Numb3rs:

1.El sou setmanal.

Després de fer càlculs, he arribat a la conclusió de que l'opció B alcançarà a l'opció A.

A les 10 setmanes tenim que amb l'opció A és guanyaríen 100$, i que amb l'opció B 5'12$, i és molta diferéncia, però hi ha que pensar que a l'opció A cada setmana que passa se li sumen 10$, i a l'opció B, cada setmana que passa se li suma el doble que l'anterior, per aquesta raó jo he anant fent calculs a partir de la setmana 10:

opció A:

11:110$

12:120$

13:130$

14:140$

15:150$

16:160$

opció B:

11:10'24$

12:20'48$

13:40'96$

14:81'92$

15:122'88$

16:245'76$

Doncs, que a la setmana 16 l'opció B, ja superarà a la A.

I la suma?

En aquesta segona activitat he fet el mateix, una gràfica, amb dos taules de valors, però sumant-li a cada valor de diners, la suma del anterior, i he vist que l'opció B alcança a l'opció A en la setmana 17.

    

poquet a poquet.

Triangle més económic:

Mantín fixa la base, mou D. Quin triangle té el menor perímetre?El triangle amb menor períumetre,és un triangle isoscel·les, amb base 2. alçaria 5 i perímetre 12'2cm.

Canvia el valor de la base. Quin triangle té el menor perímetre?El triangle amb menor perímetre si canviem la base, és un triangle isosel·les amb base 3'3,alçària 3'03cm i perímetre 10'2cm.

Rectangle més barat:

Quin és el major valor possible de la base? I el menor?

La base amb major valor és 11'34cm, i la base amb menor valor és 0'02.

Quin rectangle té perímetre mínim?

El rectangle que té de base 2'24cm,alçària 2'23cm i el perímetre 8'94cm.

Fes una taula on poses almenys 20 valors de la base, el corresponent valor de l'alçària i el perímetre.

             Base                                Alçària                              Perímetre

4’68	1’07	11’5
0’2	24’7	49’81
3’52	1’42	9’88
7’44	0’67	16’22
2’69	1’86	9’1
11’34	0’44	23’55
7’57	0’66	16’36
4’35	1’15	10’99
3’72	1’34	10’13
1’41	3’54	9’91
8’36	0’6	17’91
5’76	0’87	13’25
1’84	2’72	9’12
0’38	13’1	26’97
4	1’25	10’5
6’7	0’75	14’89
0’96	5’19	12’3
9’41	0’53	19’88
10’26	0’46	21’49
11’11	0’45	23’12

Representa gràficament les relacions base-alçària i base-perímetre.

1er pas:

2on pas:

Taula més gran:

2ª gràfica:

Taula més clara:

• Podries trobar la fórmula que relaciona l'alçària (a) amb la base (b)?(A1,B1)

I la que relaciona el perímetre (P) amb la base (b)?no. 

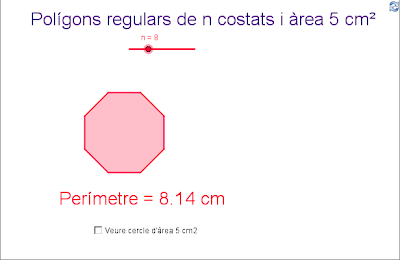
La figura plana més econòmica

I ara, passant per diversos polígons regulars, arribarem a concloure quina és, de totes les figures planes que tenen igual àrea, la de menor perímetre. 
Tots els polígons tenen 5 cm2 d'àrea. El nombre de costats es pot modificar amb el botó lliscant. 
Què ocorre amb el perímetre si augmenta el nombre de costats? Que disminueix.                             Triangle:

Quadrat:

Pentagon:

Exagon:

Heptagon:

Hoptogon:

Eneagon:

Decagon:

                                         Dodecaedre:

                                   Dodecàgon:

                                            Tridecàgon:

                                        Tetradecàgon:

                                      Pentadecàgon:

                                     Hexadecàgon:

                                     Heptadecàgon:

                                       Optadecàgon:

                                     Eneadecàgon:

                                      Isodecàgono:

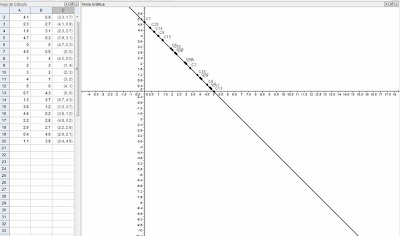
Dibuixa una gràfica que relacione nombre de costats (eix horitzontal) amb perímetre del polígon (eix vertical). Com evoluciona? 

La taula més ampliada;

La gràfica més ampliada:

Quina és la figura de perímetre mínim entre totes les figures planes de 5 cm2 d'àrea? Descriu-la per complet 

Optimitzar triangles:

El triangle té perímetre 10 cm. Pots modificar la longitud de dos costats, ja que el tercer costat està determinat pel perímetre.

Fes que la longitud dels costat b siga 2 cm, i fes variar la longitud del costat 'a'. Quin triangle té àrea màxima? El triangle que té area màxima, és un triangle inssoscel·les amb la lon''a'' de 4cm, i l'àrea de 3'87cm.

Ara, repeteix el procediment amb longitud de 'b' 3 cm Lb= 3'5 L= 4'74cm.

Fes-ho més vegades, canviant cada vegada el valor de la longitud de 'b'.

Quina conclusió n'extraus? Quin triangle de perímetre 10 cm té major àrea?

Després de fer-ho varies vegades, aquest resultat és el més alt que m'ha eixit:

La=3'9 Lb=3 L=3'1 A=4'57

Optimitzar rectangles:

El rectangle té perímetre 10 cm. Pots modificar la longitud de la base; l'alçària està determinada pel perímetre.

Quin rectangle té àrea màxima?

Lb= 2'6 Lc=2'4 A=6'24

Fes una taula on poses almenys 20 valors de la base, el corresponent valor de l'alçària i el de l'àrea. (Una taula amb tres columnes)

      Lb.                                           Lc.                                        Àrea.

3’3	1’7	5’61
4’1	0’9	3’69
2’3	2’7	6’21
1’9	3’1	5’89
4’7	0’3	1’41
0	5	indefinida
4’5	0’5	2’25
1	4	4
2	3	6
3	2	6
4	1	4
5	0	Indefinida
0’7	4’3	3’01
1’3	3’7	4’81
3’8	1’2	4’56
4’8	0’2	0’96
2’2	2’8	6’16
2’9	2’1	6’09
0’4	4’6	1’84
1’1	3’9	4’29

Representa gràficament les relacions base-alçària i base-àrea.
                                        base/alçària

base/area

Optimitzar pentàgons.

Quin pentàgon té àrea màxima? (Ve expressada en centímetres quadrats, evidentment)

A mí m'ix que aquesta fígura és la que té màxima àrea,5'76.

Compara-la amb l'àrea màxima del triangle i del rectangle (tots tres tenen perímetre 10 cm, recorda-ho). Quina àrea és major?

                                                  ?????

La millor figura plana.

De totes les figures planes, la figura òptima és aquella que té l'àrea màxima entre totes les figures amb el mateix perímetre, o el mínim perímetre entre totes les figures amb la mateixa àrea.
Deprés de fer l'estudi d'algunes figures (triangle, rectangle, pentàgon), ja et pots imaginar quina és la figura òptima.
Per si encara tens dubtes, pots utilitzar aquesta construcció.